1 で示した多段階反応のエネルギー準位図を示す(エネルギー準位は任意の高さを選んでいる).
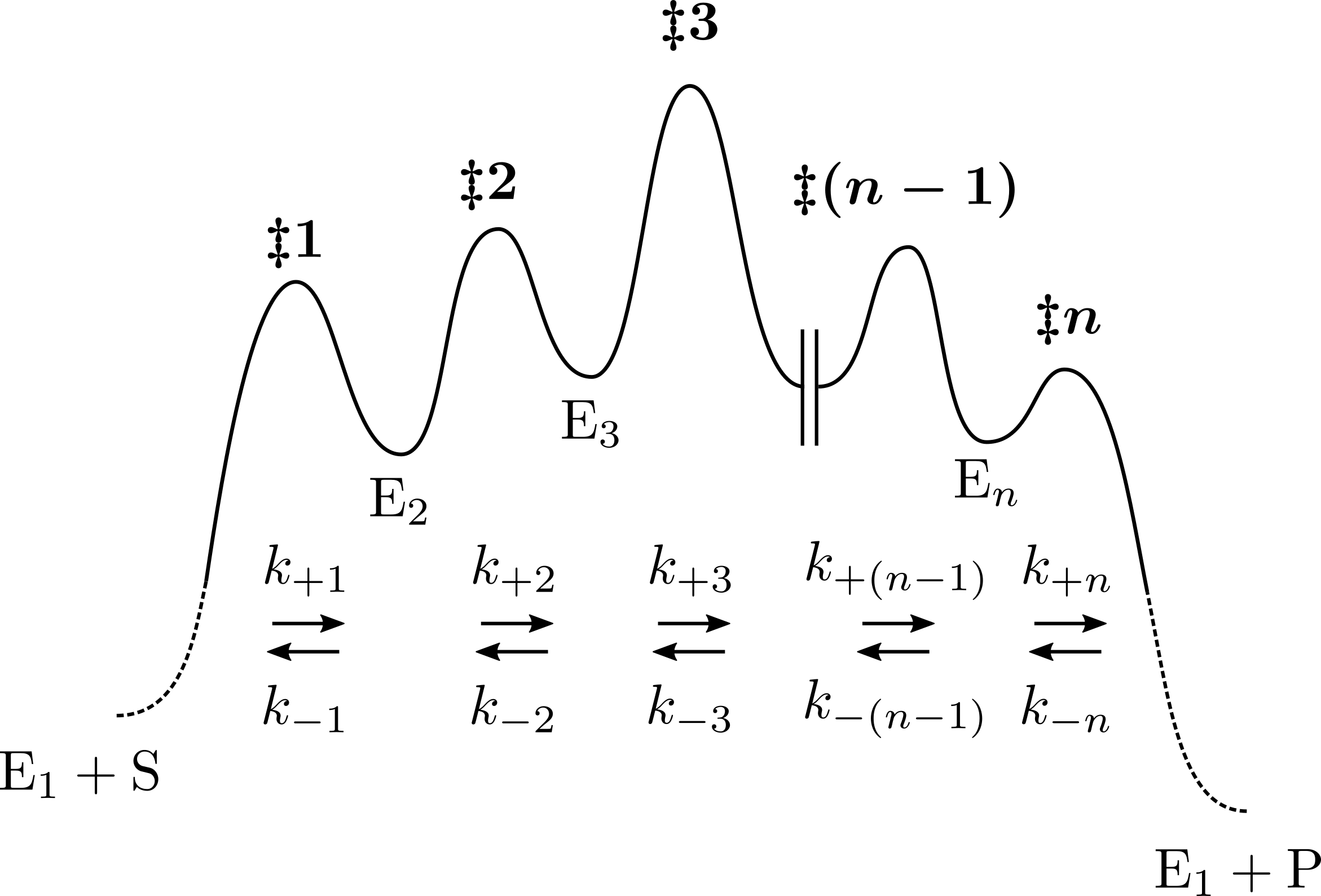
$k_{\mathrm{cat}}/K_{\mathrm{m}}$ の式を再掲し,変形すると, \begin{align} \frac{k_{\mathrm{cat}}}{K_{\mathrm{m}}} & =\frac{1}{{\displaystyle \frac{1}{k_{+1}}+\frac{k_{-1}}{k_{+1}}\frac{1}{k_{+2}}+\cdots+\frac{k_{-1}}{k_{+1}}\frac{k_{-2}}{k_{+2}}\cdots\frac{k_{-(n-1)}}{k_{+(n-1)}}\frac{1}{k_{+n}}}}\\ & = \frac{1}{{\displaystyle \frac{1}{k_{+1}}\left(1+\frac{k_{-1}}{k_{+2}}+\frac{k_{-1}}{k_{+2}}\frac{k_{-2}}{k_{+3}}\cdots+\frac{k_{-1}}{k_{+2}}\frac{k_{-2}}{k_{+3}}\cdots\frac{k_{-(n-1)}}{k_{+n}}\right)}} \end{align}
$k_{+1}$ に Eyring の式を適用して, \begin{align} k_{+1}=\frac{k_{\mathrm{B}}T}{h}\frac{[\ddagger\boldsymbol{1}]}{[\mathrm{E}_1][\mathrm{S}]} \end{align} これを式 (2) に代入して, \begin{align} \frac{k_{\mathrm{cat}}}{K_{\mathrm{m}}}=\frac{k_{\mathrm{B}}T}{h}\frac{1}{{\displaystyle \frac{1}{[\ddagger\boldsymbol{1}]}+\frac{1}{[\ddagger\boldsymbol{1}]}\frac{k_{-1}}{k_{+2}}+\frac{1}{[\ddagger\boldsymbol{1}]}\frac{k_{-1}}{k_{+2}}\frac{k_{-2}}{k_{+3}}\cdots+\frac{1}{[\ddagger\boldsymbol{1}]}\frac{k_{-1}}{k_{+2}}\frac{k_{-2}}{k_{+3}}\cdots\frac{k_{-(n-1)}}{k_{+n}}}}\frac{1}{[\mathrm{E}_1][\mathrm{S}]} \end{align} $k_{-1}$ および $k_{+2}$ に Eyring の式を適用して, \begin{align} k_{-1}&=\frac{k_{\mathrm{B}}T}{h}\frac{[\ddagger\boldsymbol{1}]}{[\mathrm{E}_2]}\\ k_{+2}&=\frac{k_{\mathrm{B}}T}{h}\frac{[\ddagger\boldsymbol{2}]}{[\mathrm{E}_2]} \end{align} より, \begin{align} \frac{k_{-1}}{k_{+2}}=\frac{[\ddagger\boldsymbol{1}]}{[\ddagger\boldsymbol{2}]} \end{align} これを順次用いることにより,式 (4) は \begin{align} \frac{k_{\mathrm{cat}}}{K_{\mathrm{m}}}=\frac{k_{\mathrm{B}}T}{h}\frac{1}{{\displaystyle \frac{1}{[\ddagger\boldsymbol{1}]}+\frac{1}{[\ddagger\boldsymbol{2}]}+\frac{1}{[\ddagger\boldsymbol{3}]}\cdots+\frac{1}{[\ddagger\boldsymbol{ n}]}}}\frac{1}{[\mathrm{E}_1][\mathrm{S}]} \end{align} という簡単な形になる.この分母に注目し,各遷移状態濃度の調和平均 \begin{align} [\mathrm{\ddagger\mathrm{TS}}]_{\mathrm{H}}=\frac{n}{{\displaystyle \frac{1}{[\ddagger\boldsymbol{1}]}+\frac{1}{[\ddagger\boldsymbol{2}]}+\frac{1}{[\ddagger\boldsymbol{3}]}\cdots+\frac{1}{[\ddagger\boldsymbol{ n}]}}} \end{align} を用いると,式 (8) は \begin{align} \frac{k_{\mathrm{cat}}}{K_{\mathrm{m}}}=\frac{k_{\mathrm{B}}T}{h}\frac{1}{n}\frac{[\ddagger\mathrm{TS}]_{\mathrm{H}}}{[\mathrm{E}_1][\mathrm{S}]} \end{align} となる.すなわち,$k_{\mathrm{cat}}/K_{\mathrm{m}}$ は基質の濃度が十分に低いときに酵素と基質が出会って遷移状態を経て酵素と生成物に変化すると考えた場合の二次反応速度定数であるが,その遷移状態を仮想的に 1 つのものと見なした場合,その遷移状態の濃度は実際の遷移状態の濃度の調和平均を遷移状態の数で割ったものになる,ということになる.
次に $k_{\mathrm{cat}}$ についても同様に $i$ ごとに $1/k_{+i}$ で括り,順次遷移状態の濃度に変換して行くことにより, \begin{align} k_{\mathrm{cat}}=\frac{k_{\mathrm{B}}T}{h}\frac{1}{{\displaystyle \frac{1}{[\ddagger\boldsymbol{2}]}+\frac{2}{[\ddagger\boldsymbol{3}]}+\frac{3}{[\ddagger\boldsymbol{4}]}\cdots+\frac{n-1}{[\ddagger\boldsymbol{n}]}}}\frac{1}{[\mathrm{E}_{2}]} \end{align} が得られる.この場合は各遷移状態の重み付き調和平均 \begin{align} [\mathrm{\ddagger\mathrm{TS}}]_{\mathrm{WH}}=\frac{{\displaystyle \sum_{i=1}^{n-1}i}}{{\displaystyle \frac{1}{[\ddagger\boldsymbol{2}]}+\frac{2}{[\ddagger\boldsymbol{3}]}+\frac{3}{[\ddagger\boldsymbol{4}]}\cdots+\frac{n-1}{[\ddagger\boldsymbol{n}]}}} \end{align} を用いることにより,式 (11) は \begin{align} k_{\mathrm{cat}}=\frac{k_{\mathrm{B}}T}{h}\frac{1}{{\displaystyle \sum_{i=1}^{n-1}}}\frac{[\ddagger\mathrm{TS}]_{\mathrm{WH}}}{[\mathrm{E}_{2}]} \end{align} となる.すなわち,$k_{\mathrm{cat}}$ は Michaelis 複合体 $\mathrm{E}_2$ から遷移状態を経て酵素と生成物に変化すると考えた場合の一次反応速度定数であるが,この遷移状態を仮想的に 1 つのものと見なした場合,その遷移状態の濃度は $\ddagger\boldsymbol{2}$ 以降の実際の遷移状態の濃度の重み付き調和平均を $\sum_{i=1}^{n-1}$ で割ったものになる.
ここで調和平均が登場したことについて考察しよう.調和平均の意味を理解するための例としてよく用いられるのが,往きと帰りで異なる速さで目的地まで往復する場合の平均の速さである.これを計算すると実感としてわかるが,調和平均は少ない数の方に引きずられる.そうすると,律速段階と関連付けることにより,調和平均が $k_{\mathrm{cat}}/K_{\mathrm{m}}$ と $k_{\mathrm{cat}}$ の中に現れることが理解されよう.また,調和平均のままであれば式 (9) の $n$ や式 (12) の $\sum_{i=1}^{n-1}$ が掛けられてしまうが,式 (10) や式 (13) で示されるようにこれらで割ることによって,たとえば突出して濃度の低い遷移状態があれば,その濃度が $[\ddagger{\mathrm{TS}}]_{\mathrm{H}}$ や $[\ddagger{\mathrm{TS}}]_{\mathrm{WH}}$ に一致するようになっている.
また,$k_{\mathrm{cat}}$ では重み付き調和平均となっているが,後ろの遷移状態ほど重みが大きくなっていることは興味深い.このことは,$k_{\mathrm{cat}}/K_{\mathrm{m}}$ や $k_{\mathrm{cat}}$ を上昇させるためには遷移状態の安定化が重要であるが, $k_{\mathrm{cat}}$ の場合は反応の後ろの方の遷移状態に注力した方が効果的であることを意味している可能性がある.
このように定常状態の反応速度論的パラメータとして $k_{\mathrm{cat}}/K_{\mathrm{m}}$ と $k_{\mathrm{cat}}$ はエネルギー準位図と関連づけて考えることができるが,$K_{\mathrm{m}}$ はそのような関連付けは困難であることがわかる.
なお,式 (9) や式 (12) で登場する遷移状態の濃度は反応が平衡に達したときの濃度であり,実際の定常状態の時の濃度とは異なることは注意しておく必要がある.これについては稿を改めて書く.